DeepLearning｜関数

はじめに

こんにちは！Palmです😊

最近、ChatBotなどを作っているとディープラーニングについても理解したいと思うようになりました🤖💬 そこで今日は、微分積分の関数について解説します🌟

このブログではJupyter Notebookを使います。

ダウンロードの仕方や、使い方はこちらのブログから↓

合わせて読みたい

Jupyter Notebookの基本

関数って何？

機械学習やディープラーニングを理解するためには「損失関数（Loss function）」の値を最小にすることが大切みたいです。そのために使うのが「勾配降下法（Stochastic Gradient Descent, SGD）」です。このアルゴリズムの根本には微分の考え方があるんです。微分の理解なくしてディープラーニングの理解はありえません！📚✨

微分積分に入る前に、まずは、「関数」について確認しましょう！関数は、ある入力値に対して一つの出力値を返すルールです。例えば、こんな感じです：

1入力 → 関数F → 出力
2 1   →  F  →  2
3 2   →  F  →  5

関数の概念を模式的に書いたものです。中央にある箱が関数です。この箱は実数値を一つ入力として受け付け、実数値を一つ出力する働きを持っています。

例えば、

1入力値:1→出力値:2
2入力値:2→出力値:5

と言った感じです。

この例では、関数Fは次のように表現できます：

1F(1) = 2
2F(2) = 5

上の振る舞いだけでは、この関数がどういう仕組みで返しているのかはわかりませんが、一番下に種明かしの式がかかれています！

実数値の入力値を $x$ とすると、出力値は $x^2 + 1$ という計算式で計算されます。例えば、$x=1$ を代入すると値 2 が、$x=2$ を代入すると値 5 が得られます。

この種明かしの仕組みを数式で表現すると次のようになります：

$$ F(x) = x^2 + 1 $$

関数のプログラム例

1def f(x):
2    return x**2 + 1

In（実行したいソースコード）

1f(1)

Out（そのコードの出力結果）

12

In

1f(2)

Out

15

関数のグラフって？

関数のグラフは、関数に様々な入力値を代入したときの出力値を二次元平面上にプロットしたものです。これにより、関数の挙動や特徴を視覚的に理解することができます。まるで魔法みたいですよね！✨🧙‍♂️

グラフの描き方

例えば、関数 f(𝑥)=x^2+1 のグラフを描くために、次の手順を踏みます。

実際のプログラム例

以下のプログラムは、関数 f(x)=x^2+1 のグラフを描く例です。Pythonのnumpyとmatplotlibを使っています。

1import numpy as np
2import matplotlib.pyplot as plt

1def f(x):
2    return x**2 + 1

点(x, f(x))のプロット:

1# 点(x, f(x))のプロットとy=f(x)のグラフx1 = np.linspace(-3, 3, 7)  # -3から3までの7点のxの値を生成
2y1 = f(x1)  # 各xの値に対するf(x)の値を計算
3plt.figure(figsize=(6,6))  # グラフのサイズを設定
4plt.ylim(-2,10)  # y軸の範囲を設定
5plt.plot([-3,3],[0,0],c='k')  # x軸を描画
6plt.plot([0,0],[-2,10], c='k')  # y軸を描画
7plt.scatter(x1,y1,c='k',s=50)  # 点(x, f(x))をプロット
8plt.grid()  # グリッドを表示
9plt.xlabel('x', fontsize=14)  # x軸のラベルを設定
10plt.ylabel('y',fontsize=14)  # y軸のラベルを設定
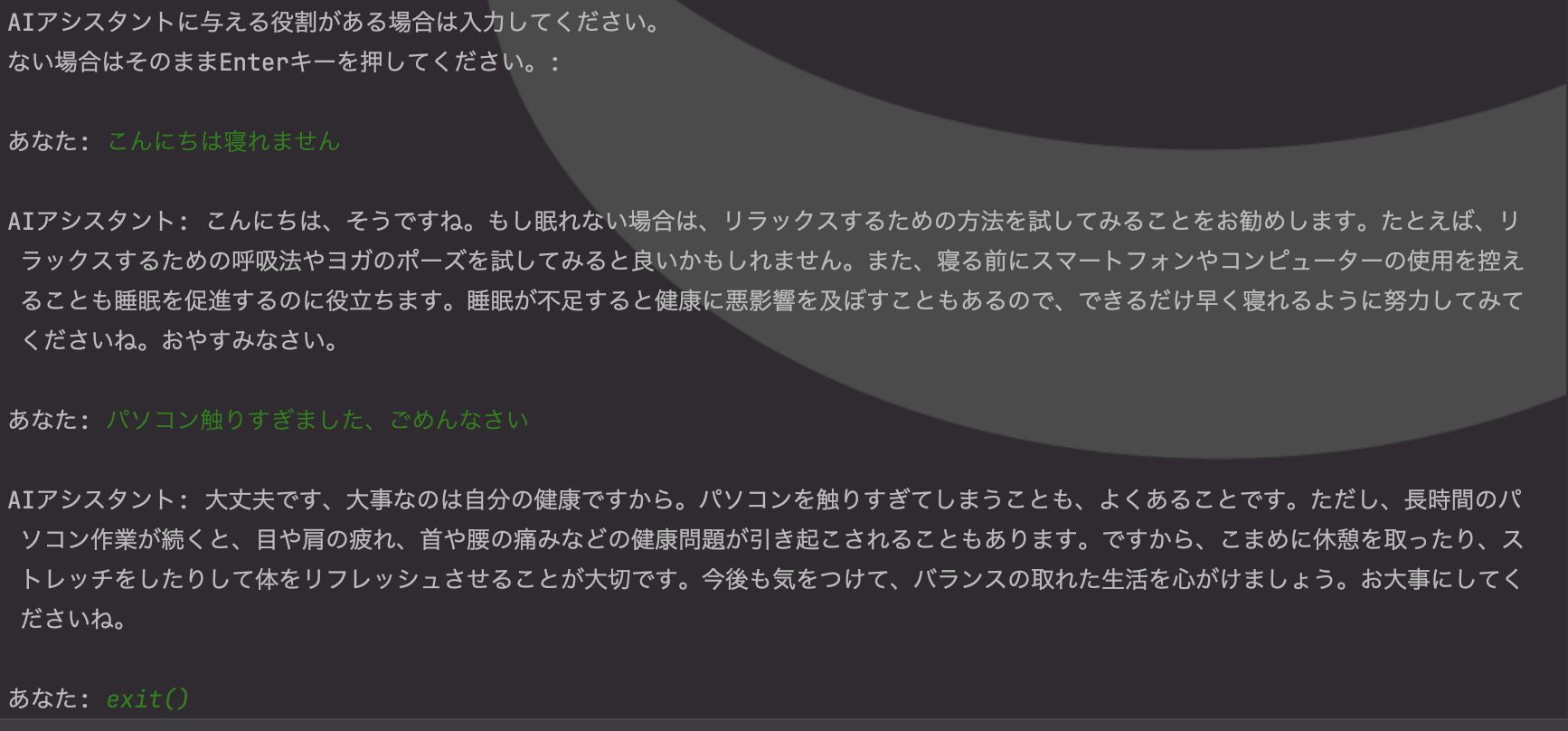
11plt.show()  # グラフを表示

点(x, f(x))のプロット:
x = -3から3までの7点での関数の出力値をプロットします。関数の大まかな挙動を確認できます。

さらに細かい点(x, f(x))のプロット:

1# 点(x, f(x))のプロットとy=f(x)のグラフ
2x2 = np.linspace(-3, 3, 31)  # -3から3までの31点のxの値を生成
3y2 = f(x2)  # 各xの値に対するf(x)の値を計算
4
5plt.figure(figsize=(6,6))  # グラフのサイズを設定
6plt.ylim(-2,10)  # y軸の範囲を設定
7plt.plot([-3,3],[0,0],c='k')  # x軸を描画
8plt.plot([0,0],[-2,10], c='k')  # y軸を描画
9plt.scatter(x2,y2,c='k',s=50)  # 点(x, f(x))をプロット
10plt.grid()  # グリッドを表示
11plt.xlabel('x', fontsize=14)  # x軸のラベルを設定
12plt.ylabel('y',fontsize=14)  # y軸のラベルを設定
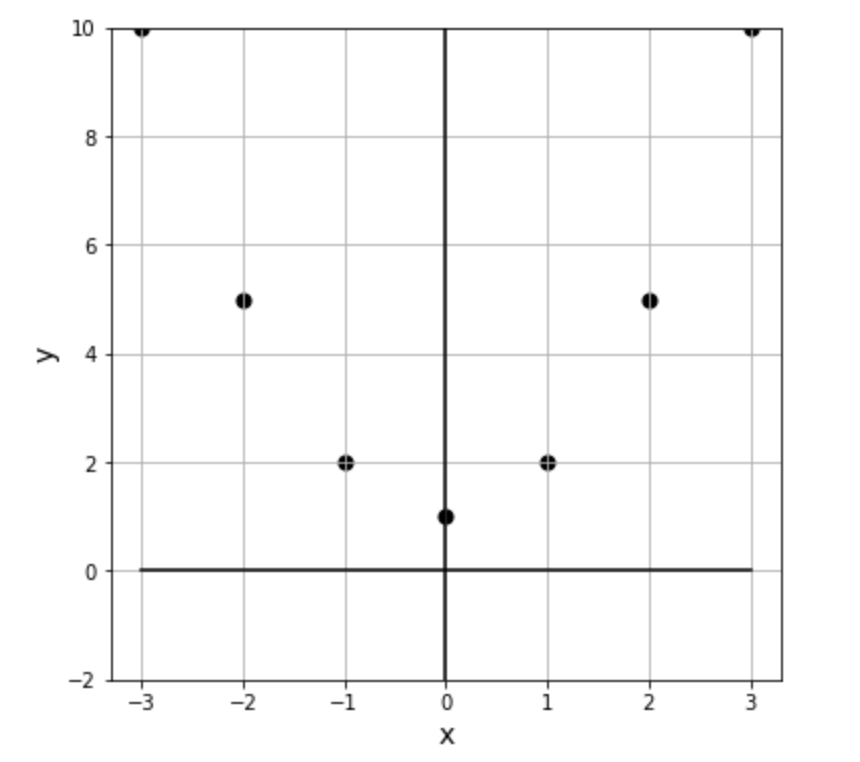
13plt.show()  # グラフを表示

さらに細かい点(x, f(x))のプロット:
x = -3から3までの31点での関数の出力値をプロットします。より詳細な挙動がわかります。

連続的な関数のグラフ:

1x = np.linspace(-3, 3, 601) # -3から3までの601点のxの値を生成
2y = f(x) # 各xの値に対するf(x)の値を計算
3plt.figure(figsize=(6,6))  # グラフのサイズを設定
4plt.plot(x,y,c='k')  # 関数f(x)のグラフを描画
5plt.ylim(-2,10)  # y軸の範囲を設定
6plt.plot([-3,3],[0,0],c='k')  # x軸を描画
7plt.plot([0,0],[-2,10], c='k')  # y軸を描画
8plt.scatter([1,2],[2,5],c='k',s=50)  # 特定の点(x, f(x))をプロット
9plt.grid()  # グリッドを表示
10plt.xlabel('x', fontsize=14)  # x軸のラベルを設定
11plt.ylabel('y',fontsize=14)  # y軸のラベルを設定
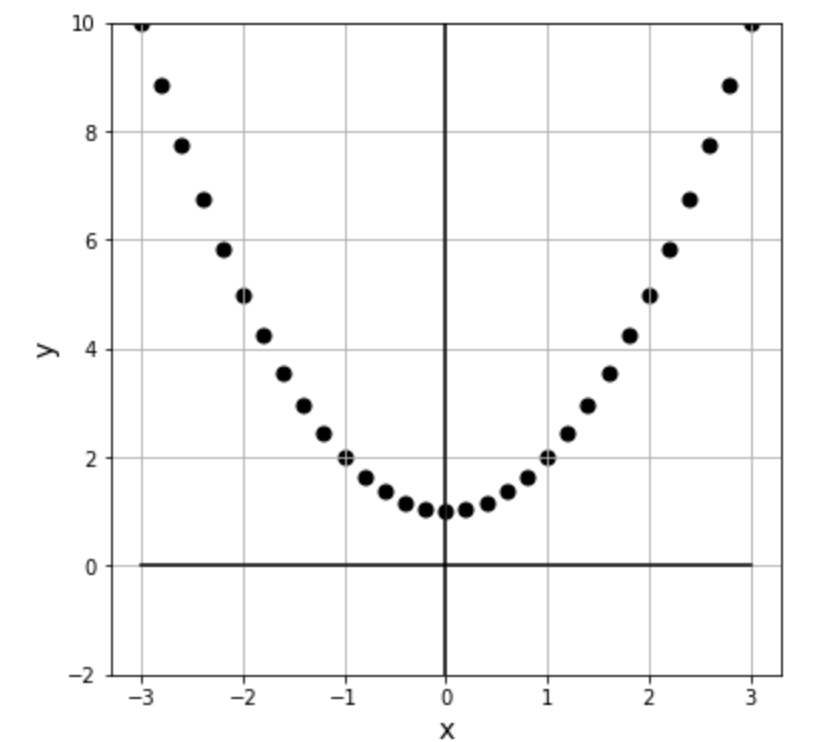
12plt.show()  # グラフを表示

連続的な関数のグラフ:
x = -3から3までの連続的な値に対する関数の出力値を描画します。関数の全体像がわかります。

このように、関数のグラフを描くことで、その関数の挙動や特徴を視覚的に理解することができます。また、関数の変化を直感的に掴むことができ、機械学習やディープラーニングの理解に役立ちます😊

専門用語の詳細解説

損失関数（Loss function）

損失関数とは、モデルの予測値と実際の値との誤差を数値化したものです。この誤差が大きいほど、モデルの予測が実際と異なっていることを示します。ディープラーニングでは、この損失関数の値をできるだけ小さくすることで、モデルの予測精度を高めようとします。

例えば、回帰問題では「平均二乗誤差（Mean Squared Error, MSE）」がよく使われます。これは、予測値と実際の値の差を二乗し、それを平均したものです。分類問題では「クロスエントロピー（Cross-Entropy）」が一般的のようです。

勾配降下法（Stochastic Gradient Descent, SGD）

勾配降下法は、損失関数の値を最小にするパラメータを見つけるためのアルゴリズムです。この方法では、損失関数の勾配（傾き）を計算し、その方向に少しずつパラメータを更新していきます。これを繰り返すことで、最適なパラメータを見つけることができます。

SGDは、大量のデータを少しずつ使ってパラメータを更新するため、計算効率が高く、特に大規模なデータセットに適しています。他にも、ミニバッチ勾配降下法やバッチ勾配降下法といった変種があります。

微分の重要性

微分とは、関数の変化率を求める数学的手法です。具体的には、関数のグラフの接線の傾きを求めることです。勾配降下法では、この傾き（勾配）を使って損失関数の最小値を探します。つまり、微分を理解することで、どの方向にパラメータを更新すれば良いのかがわかるのです。

例えば、関数 f(x)=x^2の微分を求めるとf′(x)=2x となります。この微分値を使って、xの値がどの方向に変化すれば関数の値が小さくなるかを判断します。

関数のグラフについて、これで理解が少し深まった気がします。ディープラーニングを学ぶ上で関数や微分の理解は非常に重要です。

最後まで読んでいただきありがとうございました！

Palm

東京通信大学

XContact

Blogger✍Developer🛠Designer👩‍💻様々な言語に特化😏語学とプログラミングを学べる外語ビジネス専門学校を卒業後、東京通信大学に編入。中国語が好き。ICPC参加歴あり。これまで長期webインターンに参加し、現在長期iOSインターンに参加中である。ハッカソン2連続受賞中。