DeepLearning｜合成関数と逆関数

こんにちは！palmです🌟

今日はディープラーニングに欠かせない微分積分のお話、第2弾です📚✨。昨日は関数についてお話ししましたが、今回は合成関数と逆関数について解説します。これらはディープラーニングを理解するための重要な概念ですよ💡

第一弾はこちらです。

合わせて読みたい

DeepLearning｜関数

環境

このブログではJupyter Notebookを使います。

ダウンロードの仕方や、使い方はこちらのブログから↓

合わせて読みたい

Jupyter Notebookの基本

合成関数ってなに？🤔

まず、合成関数について説明しましょう。合成関数は、ある関数の出力を別の関数の入力として利用することで新しい関数を作るものです。ディープラーニングでは非常によく使われる基本原理なんです🎓

例で見てみましょう🔍

例えば、次の2つの関数があるとします：

$$
f(x) = x^2 + 1
$$

$$
g(x) = \sqrt{x}
$$

この時、関数 $f(x)$ の出力を関数 $g(x)$ の入力とすることで、新しい関数を作ることができます。これが合成関数です。

$$
h(x) = g(f(x)) = \sqrt{x^2 + 1}
$$

このように、合成関数は一見複雑な関数の微分を簡単にするために使われます。例えば、 $h(x) = \sqrt{x^2 + 1}$ の微分を直接求めるのは難しいですが、 $f(x) = x^2 + 1$ と $g(x) = \sqrt{x}$ の組み合わせで考えると簡単に微分ができます🧮

なぜ $g \circ f(x)$ なの？

関数の合成を表すとき、$g \circ f(x)$ という表記になります。この表記はなぜかというと、数式上でデータは右から左に流れるからです。具体的には次のようになります：

$$
x \rightarrow f(x) \rightarrow g(f(x))
$$

つまり、$x$ に関数 $f$ を適用して、その結果を関数 $g$ に渡すという流れです。これを数式で表すと $g(f(x))$ となります。

逆関数とは？🔄

次に逆関数について説明します。逆関数とは、ある関数の出力を元に戻す関数のことです。例えば、関数 $f(x)$ の逆関数を $f^{-1}(x)$ と表します。

例で見てみましょう🔍

関数 $f(x) = x^2 + 1$ を考えます。この関数の逆関数を求めるには、次のステップを踏みます：

1. 元の関係式 $y = x^2 + 1$ で $x$ と $y$ を入れ替えます。
2. 新しい式 $x = y^2 + 1$ を $y$ について解きます。

すると、

$$
x = y^2 + 1
$$

$$
y^2 = x – 1
$$

$$
y = \sqrt{x – 1}
$$

これが $f(x) = x^2 + 1$ の逆関数 $f^{-1}(x) = \sqrt{x – 1}$ です。ただし、この逆関数が定義できるためには、$x$ の範囲を限定する必要があります。例えば、$x \geq 0$ の場合には、この逆関数が一意に定まります。

逆関数のグラフ📈

逆関数 $g(x) = f^{-1}(x)$ のグラフは、元の関数 $y = f(x)$ のグラフと直線 $y = x$ に関して対称な形になります。これは、点 $(a, b)$ が $y = f(x)$ のグラフ上の点であれば、$f(a) = b$ であり、逆関数の定義から $g(b) = a$ となるためです。

例えば、関数 $f(x) = x^2 + 1$ とその逆関数 $g(x) = \sqrt{x – 1}$ のグラフを描くと、次のようになります：

1import numpy as np  # 数値計算ライブラリnumpyをインポート
2import matplotlib.pyplot as plt  # グラフ描画ライブラリmatplotlibをインポート
3
4def f(x):
5    return x**2 + 1  # 関数f(x) = x^2 + 1を定義
6
7def g(x):
8    return np.sqrt(x - 1)  # 関数g(x) = √(x - 1)を定義
9
10xx1 = np.linspace(0.0, 4.0, 200)  # 0から4までを200分割したxの値を生成
11xx2 = np.linspace(1.0, 4.0, 200)  # 1から4までを200分割したxの値を生成
12yy1 = f(xx1)  # xx1に対するf(x)の値を計算
13yy2 = g(xx2)  # xx2に対するg(x)の値を計算
14
15plt.figure(figsize=(6,6))  # グラフのサイズを指定
16plt.xlabel('x', fontsize=14)  # x軸のラベルを設定
17plt.ylabel('y', fontsize=14)  # y軸のラベルを設定
18plt.ylim(-2.0, 4.0)  # y軸の表示範囲を設定
19plt.xlim(-2.0, 4.0)  # x軸の表示範囲を設定
20plt.grid()  # グリッドを表示
21plt.plot(xx1, yy1, linestyle='-', c='k', label='y=x^2+1')  # f(x)のグラフを描画
22plt.plot(xx2, yy2, linestyle='-', c='k', label='y=√(x-1)')  # g(x)のグラフを描画
23plt.plot([-2,4],[-2,4], color='black')  # 直線y=xを描画
24plt.plot([-2,4],[0,0], color='black')  # x軸を描画
25plt.plot([0,0],[-2,4], color='black')  # y軸を描画
26plt.legend(fontsize=14)  # 凡例を表示
27plt.show()  # グラフを表示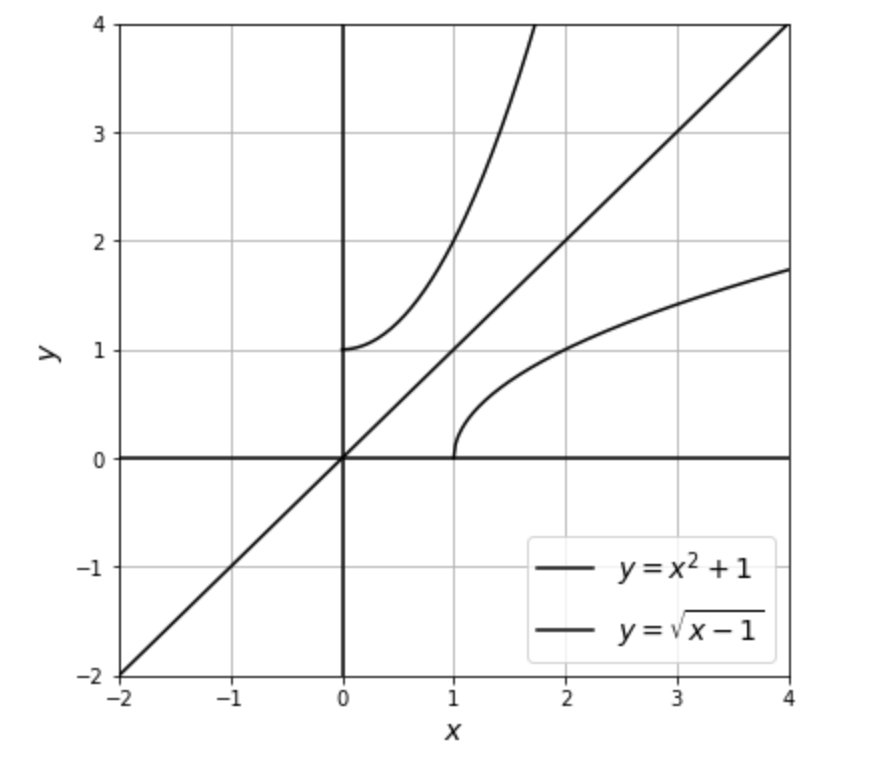

• $f(x)$ のグラフ上の点 $(a, b)$ は、$y = x$ の直線に関して対称な点 $(b, a)$ が $g(x)$ のグラフ上にあります。

まとめ🎉

今日は合成関数と逆関数についてお話ししました。これらの概念はディープラーニングだけでなく、数学全般において非常に重要です。合成関数を理解することで複雑な関数の微分が簡単にでき、逆関数を理解することで関数の逆操作が可能になります。これからも一緒に学んでいきましょう🌟

次回はさらに深掘りして、もっとディープな話題に挑戦します。お楽しみに✨

質問やリクエストがあれば、ぜひコメントで教えてくださいね😊

それでは、またね〜👋💫

Palm

東京通信大学3年生

XContact

私はpalm(ぱるむ）です。お花や自然が大好きです。専門学校でWeb開発を学び、東京通信大学に編入しました。得意分野は、ウェブ開発（フロントエンド、バックエンド）や機械学習（自然言語、データ分析）です。趣味で色々デモ開発をしています。